X 66
North Suburban HAMMOND ORGAN Service
The three typical waveforms used in electronic organs.
These are the three basic types of electrical waveforms which we find in many analog electronic organs. For best results, an instrument should make use of all three where necessary. Filtering circuits can transform both sawtooth and square waves into very good sine waves, and a clipping circuit can make a reasonably good square wave from a sine wave.
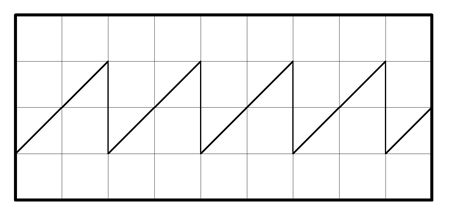
Figure 1. A sawtooth wave. It contains all harmonics, in phase, and the amplitude of each is inversely proportional to its ordinal number, that is, the second harmonic is 50% of the amplitude of the first or fundamental, the third harmonic's amplitude is 33.3% of that of the fundamental, etc. In a theoretically perfect sawtooth wave, the number of harmonics is infinite. In a real, practical sawtooth, perhaps no more than 50 harmonics are present.
For authentic duplication of various musical instrument sounds by analog methods, each of the three types should be available in the instrument. Sawtooth waves that pass through suitable formant filters can yield good imitations of many woodwind, string and brass instruments. Sine waves used in additive harmonic synthesis are necessary for good imitation of various percussion voices such as chimes and bells of various types. Square waves are useful for creating a "hollow" woodwind tone such as the clarinet and they are also more easily filtered down into sine waves than sawtooth waves. In many tone generating systems, it's easier to start by generating square waves and then filtering them down to sine waves rather than to create sine waves directly.
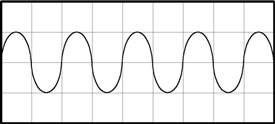
Figure 2. The sine wave is just a pure tone or pitch. It has no harmonics and no character. In an instrument such as the Hammond organ, it is used as a tonal building block to create other, different sounds when mixed with sinewaves that are harmonically related to each other.
Figure two is a sine wave. The sine wave has no upper harmonics at all. The sinewave is actually the first harmonic by itself. As a sound wave, it is just a pure, characterless tone. Sine waves are used as individual harmonic pitches in the additive harmonic synthesis system.
Figure three is a square wave. The theoretically perfect square wave contains an infinite number of odd numbered harmonics only, and like the sawtooth wave, the amplitudes of the individual harmonics are inversely proportional to their ordinal numbers, and all are in phase. A practical square wave may have usually less than 50 harmonics. In analog electronic organs, the square wave is useful for imitating certain woodwind instruments like the clarinet whose tone has the odd harmonics emphasized. It is also easy to convert a square wave into a sine wave by simple filtering.
Even though the X66 used entirely analog technology, it seems evident that musicians had a significant say in the design of this instrument, and the Hammond engineers evidently listened! Many of the competing electronic organ manufacturers used tone generators that produced square waves only. From these they would filter the square waves to make pretty decent sine waves, but they did not bother with sawtooth waves. Rather, they created what are referred to as staircase waves. These are made by superimposing octavely-related square waves. The idea was that any square wave would have only the odd harmonics. So, if you had a wave of 100Hz, then the next harmonic would be 300 Hz, and after that, 500Hz. Therefore, they would also mix in a square wave of 200Hz. Its third harmonic would be 600 Hz. So the thinking was why not just add a 200Hz square wave on top of a 100 Hz wave. At 200 Hz, it would represent the second harmonic of 100Hz. However, there would be no fourth harmonic of 400Hz unless, to carry this out further, they'd add a 400Hz wave on top of the 200 Hz wave. However, then among others, there's no eight harmonic! So you'd have to add still another square wave to the mix, this time having 800 Hz.
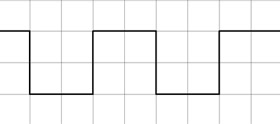
Figure 3. The square wave contains the odd number harmonics only. The amplitude of each harmonic is inversely related to its ordinal number.
If you did this two or three times, you would get a waveform that could be used to derive those sounds that were most accurately duplicated by formant filtering sawtooth waves. In practice, well, opinions vary, but I was never overly impressed with staircase wave technology. Again, it was a compromise. In theory, you'd need to staircase an infinite number of octavely-related squarewaves to make a true sawtooth. If you staircase only two or three, there will still be many significant harmonics missing in the final result.
In the X66, you'd get all three waveforms, so whatever was needed was there. This is one of the many reasons why the X66 is such a nice instrument. It was expensive, but you did indeed get a superior product.
Previous Page Page 2. Next page