Vibrato
North Suburban HAMMOND ORGAN Service
In order for the heterodyne vibrato to be truly effective in an electronic instrument, a special consideration has to be included as follows. In such an instrument, the signal is first split or sent to two different sections of the instrument's amplification circuitry. The first section just amplifies the signal. The second section amplifies and also shifts the pitch of the signal by a certain amount. For a vibrato effect, the pitch shift should be between 6 to 7 Hz, which is the normal vibrato rate. However, the signal whose pitch is shifted must be shifted in such a way that the same number of Hz are changed for all harmonics as well as for the fundamental. For a simple sine wave signal, such as I used for the illustrations on previous pages of this article, this is not a consideration.
But if we wish to add a heterodyne vibrato to a complex waveform such as a sawtooth or square wave, or the wave that represents the sound of an actual musical instrument, then we can't simply shift the pitch of the wave up 6 Hz in the normal manner, because if we did, then the second harmonic of the wave in question would be raised by 12 Hz, the third by 18 Hz, and so on. The pitch shift that we must use for this purpose raises the frequency of the soundwave and all of its harmonics by a constant number of cycles. So for example if we had a waveform which had the first three harmonics, and the frequency of the wave was A440, then a normal 6 Hz pitch shift would give us a frequency of 446 Hz for the fundamental, 892 for the second harmonic and 1338 for the third harmonic. But if we tried to combine this with the unshifted 440 Hz wave, the result would sound like two soundwaves that were somewhat out of tune, because the second harmonic would develop a heterodyne vibrato effect of 12 Hz, and the third harmonic would develop a vibrato of 18 Hz, both of which are way too fast to sound any good at all.
Those of you who are familiar with the accordion (in my opinion the most awful sounding instrument ever invented) will have heard the effect which in some versions of that instrument goes by several names including musette. In this case, two and sometimes three reeds sound together for every note, one of which is approximately 6 to 7 Hz sharper than normal pitch, and the second reed will have normal pitch. If there are three reeds, the third is usually 6 to 7 Hz flatter or lower. The resulting sound, which I understand is supposedly desirable in an accordion is actually grossly out of tune. This is the sound that will make dogs howl, cats hiss, fish pop their air bladders, pigeons stop cooing and the Dow to lose a fortune. Accordions sound bad enough anyhow, so why deliberately include something that is grossly out of tune as part of their makeup? This is probably why the following statement has become widely accepted concerning the playing of accordions. What is the definition of a true gentleman? A man who knows how to play an accordion but refrains from doing so. Anyhow, back to vibrato.
But to make an effective heterodyne vibrato that sounds good and does not sound like two out of tune notes sounding together, the pitch shift must be by the same Hz for all pitches, fundamentals and their harmonics. When we do such pitch shift of 6 Hz, then all of the harmonics likewise get a 6 Hz increase so we end up with, using the above example, a wave with a fundamental of 446 Hz, a second harmonic of 886Hz and a third harmonic of 1326 Hz. If we combine these two soundwaves together, the result will be a nice sounding heterodyne vibrato of 6 Hz.
Those of you who have some experience with modern electronic instruments, particularly synthesizers, will recognize this as ring modulation, where the frequency of a signal is shifted in this manner. This is often used to create certain bell-like effects in these instruments. In this situation, the pitch shift is considerably more than 6 Hz. However, when the shift is limited to no more than 7 Hz, then the effect becomes a very nice vibrato, and this type of vibrato is very close in effect to the unique tremolo-vibrato effect that occurs in vibraharps.
As an interesting side note to the preceding, when an AC audio signal gets an constant number of Hz shift across the board, then the harmonics are no longer true harmonics, because they are no longer integral multiples of the fundamental or first harmonic's pitch. Again using our example of A 440, its second harmonic would be 880 Hz. If we shift the pitch of this wave up to 446 Hz, then the second harmonic would follow proportionally and have to be 892 Hz, 892 being exactly two times 446. But the constant Hz pitch shift would increase both the fundamental and the second harmonic by the same amount, or in this case 6 Hz. This would give us a second harmonic of 886 Hz, which is obviously not exactly two times 446. This is the all important difference, and which is also why, in a good heterodyne vibrato, the only vibrato effect that you hear in the resulting signal is that of 6 Hz, all upper harmonics having the same vibrato rate as the fundamental.
Polyphase Vibrato
The next type of vibrato to consider is a polyphase vibrato. Interestingly, even a simple vibrato effectively becomes a polyphase vibrato as soon as the audio signal gets converted to sound and leaves the speaker(s). A polyphase vibrato, however, is produced as such electronically. The polyphase vibrato can be fairly simple or very complex. One of the best examples is the vibrato of the X66 Hammond which actually consists of two identical vibrato signals but they are of opposite phase, that is, when the pitch of one signal is increasing, the pitch of the other is decreasing. The two vibrato signals must not be combined electrically, but mixed as sound waves in the air AFTER they leave their respective speakers.
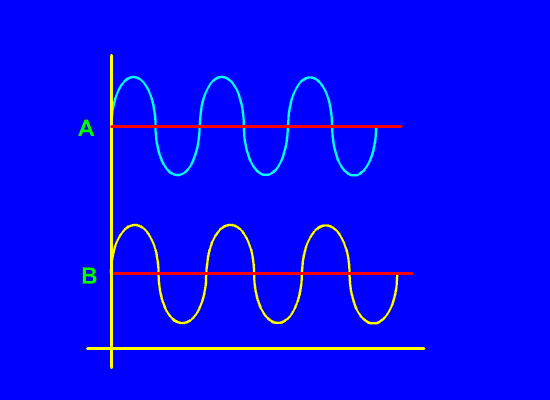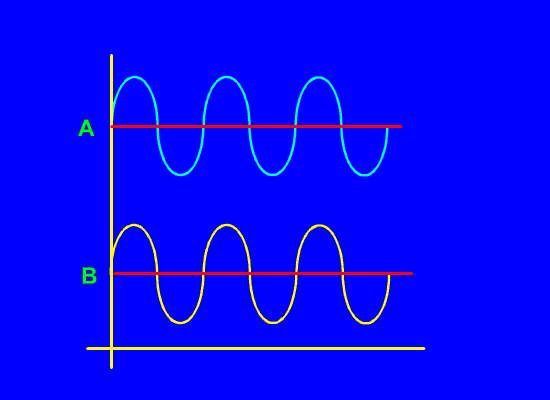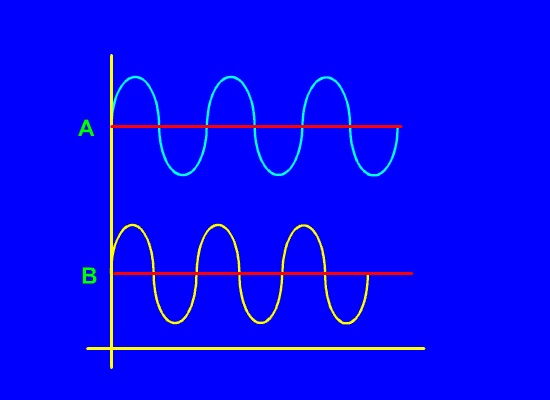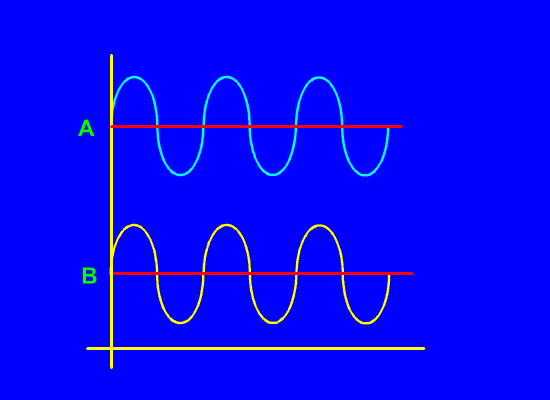
The two phase vibrato of the Hammond X66 showing how the A phase and B phase signals are in opposition; that is, when A's pitch increases, B's decreases.
Laurens Hammond at the time was adamant that Leslie speakers were not to be used with his instruments. His engineers realized that the very complex vibrato effect that a Leslie speaker produces could be simulated a lot better by using this, what Hammond referred to as dual vibrato. Modern digital signal processors can produce a number of vibratos simultaneously all of which are going either flat or sharp at different times, and this is a significant component of Leslie simulation by digital means. In the Hammond X66, the main vibrato scanner has two pickup sets of plates on its rotor which are physically spaced 180 degrees apart. Each pickup produces a single vibrato, but the physical placement of the scanner rotor pickup plates accounts for the production of two out of phase vibrato signals.
To complete the effect, they are amplified independently and sent to separate speakers. If by chance the two channels are electrically combined, the result is a very bad sounding vibrato that has double the normal rate and completely loses its musical usefulness. Thus when Hammond X66 instruments are fitted with real Leslies or wired in to large halls or arenas, great care must be taken to keep the two channels separated, and the Leslie speaker should only get either one of the vibrato channels but not both of them. Nevertheless, although simple vibrato becomes complex as soon as it leaves the speaker, a complex vibrato that is produced that way can sound remarkably like Leslie tremolo which is a real misnomer, by the way, because the Leslie effect involves infinitely complex pitch changes.
Previous Page Page 3. Next page