Wurlitzer 4600 series
North Suburban Hammond Organ Service
If we design a capacitor with one plate that can move back and forth, and connect it to a source of DC voltage, then each time the plates move together, current will flow in, and when the plates move away, current will flow out and back to the power supply, the result being an alternating current. Below we have a simple animated .gif that illustrates this principle in diagrammatic form: figure three, below, right.
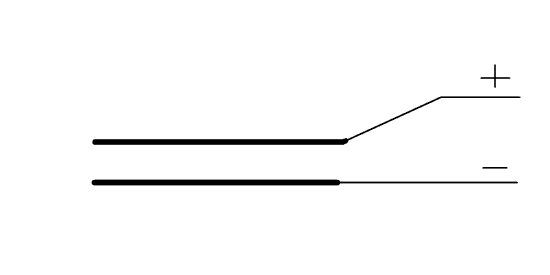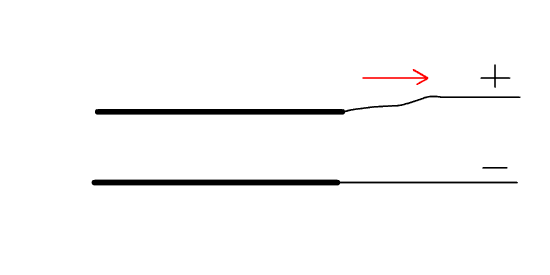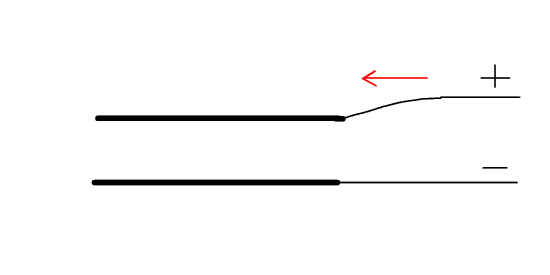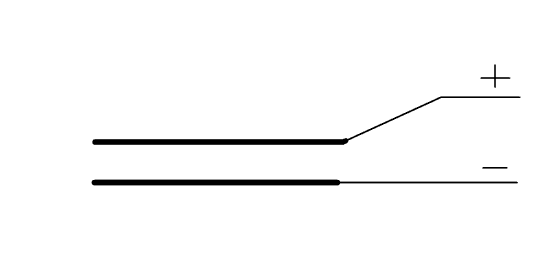
Figure 3. A capacitor with one plate that can move closer to and then farther from the other plate showing how this makes a current flow into the capacitor when the plates get closer, and out of the capacitor when they get farther apart.
The red arrow shows the direction of current flow into and out of the capacitor. Now, the question is, how could we develop a practical capacitor with a plate that moves rapidly back and forth? Well, suppose that the movable plate of the capacitor was a brass reed. Then, if air blows through the opening in the shallot and makes the reed vibrate, we have exactly what we need, a metal plate that is vibrating back and forth.
All that is necessary is to put a stationary piece of metal close to the reed and then, whenever we put a DC voltage across the reed and the stationary piece of metal, we have a vibrating, variable capacitor that will generate an alternating current waveform which can be one note of the musical scale. Furthermore, if we put our stationary piece of metal over the center of the vibrating reed, the shape of the audio frequency electrical waveform reflects the shape of the mechanical motion of the center of the reed.†
The shape of the reed's mechanical motion is not at all like the shape of the sound wave that results in the air as air blows through the shallot and vibrates the reed. The shape of the sound wave in air is what you hear from a reed in an accordion. But, because the shape of the ELECTRICAL signal that develops between the reed and the stationary piece of metal is very different when we use a reed as a variable capacitor, when we send this signal to a speaker, the resulting tone is not at all like the sound of a free reed. (More on this soon).
Another big advantage that this system gives us is that ordinarily, when we key the air supply to a reed in a musical instrument that depends on the actual sound of the air vibrating the reed, the buildup of the tone is fairly slow. In the normal mid-range of an accordion, this is still fast enough so that it is not a problem. But, when we look at the very large reeds that are required for the deep bass tones of organ pedals, it's an entirely different picture. These low bass reeds are very slow to develop their steady state sound. If we use free reeds in an organ and want to play an intricate bass line, or the bass line for a fast piece of music, we're going to be in big trouble, because these big low frequency reeds won't respond fast enough. However, if we keep the reeds vibrating continuously, and then key the voltage that we apply to the stationary pieces of metal near each reed, we can get tones that will develop essentially instantly if we so choose.
This is the basic principle of the Wurlitzer electrostatic organ. The instrument uses brass reeds as the movable plates of variable capacitors, and from these variable capacitors, generates the necessary electrical audio musical signals that become ultimately the tones or notes from its keyboards and pedals. This is why, although the instrument uses brass reeds, it is not technically a reed organ.
When we apply a DC charge to a piece of metal close to a vibrating reed, all we do is to place a charge on the capacitor which is formed by the reed and the stationary piece of metal. This is in effect a static charge, meaning that there is essentially no flow of current, only the development of a static charge across the device. Therefore, the technically correct name for a musical instrument which operates on this principle is an electrostatic instrument.
In the actual Wurlitzer instrument, each reed, depending on its frequency, has at least one, and sometimes as many as three different stationary pieces of metal close to each reed. The correct term for these stationary pieces of metal is either electrode or (Wurlitzer's term) pickup. In viewing the reeds and stationary metal parts as variable capacitors, electrode is probably the more correct term, however, to be consistent with the manufacturer, I will try to remember to refer to them as pickups for the remainder of this article.
When a particular reed has three electrodes or pickups, one is placed approximately over the center of a reed. The second one is placed over the front or vibrating end of the reed, and the third pickup is placed right before the front edge of each reed. The placement of the pickups determines the shape of the electrical signal that is generated.
From the pickups over the centers of the reeds, we get a soft, flute-like tone. It is not a pure sine wave such as the signals that a Hammond tone wheel generates, but has only a few of the lower order harmonics present and consists mainly of the first or fundamental harmonic. The pickups over the ends of the reeds generate a louder tone which has a few more harmonics. It is still essentially a flute-like tone, but several of the lower order harmonics are slightly more prominent, especially the second harmonic. The pickups that face the front edge of each reed are themselves flat pieces of sheet metal. The tones which they generate have a lot of upper harmonic development with a slight emphasis on the odd numbered harmonics, but they do not generate exclusively odd harmonics. The tone from these pickups is somewhat suggestive of a cross between that of a clarinet and a violin. Interestingly, Wurlitzer refers to these as "trumpet" tone pickups, but the tone is not even (my opinion) remotely suggestive of a trumpet.
These three basic tones are combined in various ways through the keyboards and the stop action of the instrument to produce a number of different tonalities which become the different sounds of the instrument. In some models of these ES instruments, the tones from the center pickups are used as a soft accompaniment sound on the lower keyboard, and in others, the soft accompaniment is developed by reducing the voltage on the front-end pickups and the center pickups may be used for pedal tones.
†To be technically accurate, the electrical wave that forms on a pickup which is over the center of the reed approximates the shape of the mechanical motion of the reed. However, there is some non-linearity involved here which relates to the amplitude of the excursion of the reed relative to the distance between the reed and the corresponding pickup when the reed is closest to the pickup. If the excursion distance is large compared to the distance when the reed is closest to the pickup, this will introduce non-linearity in the reed-capacitor's production of the electrical signal.
This is probably one reason why the waveform that is generated by the pickup which is over the front end of the reed has more harmonic development than the waveform given by the center pickup; because the excursion of the tip is greater than that of the middle of the reed. If the surfaces are proportionally large and the amplitude of mechanical vibration is small, then the electrical signal will be a very good replica of the mechanical motion, which is the ideal in a condenser microphone. In the Wurlitzer 4600 series organs, the surface areas of the electrodes are small, and the excursion distance of the reeds is typically greater than the distance when the reed is closest to its corresponding pickups which results in the electrical waveforms being close but not literal copies of the mechanical motion of the reeds. We can actually demonstrate this by adjusting a pickup closer to the reed and then we can hear the harmonic development in the output signal and also see the change in the waveform on a scope.
Previous Page Page 3. Next page