The HAMMOND ORGAN
North Suburban HAMMOND ORGAN Service
Note the individual transformers and capacitors which make up the filtering circuits for the generated tones. Note also that they are mounted at a 45 degree angle which minimizes inductive signal coupling between them. In the lower midrange of the instrument, the outputs pass through transformers only, and the bass pedal tones have no additional filtering circuitry although they do have copper rings placed on the coils. The copper rings suppress higher frequencies which may be present in the tones. On most Hammonds, however, the first twelve, that is the first octave of the lowest pedal bass tones are generated by special two lobe tone wheels which are shaped to give a wave which contains a few of the lower order odd numbered harmonics.
The Hammond tone generator must produce accurate sine wave signals to satisfy the instrument’s method of deriving various tone colors or different sounds. The Hammond can generate hundreds of different sounds, and each of these sounds has many subtle variations. Most musical sounds are made up of harmonics.
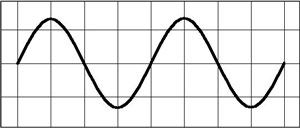
Figure 9. A sine wave, or the graphical representation of a single harmonic or one basic generated note of a Hammond organ. When sinewave tones which are harmonically related are sounded together, especially if they originate from the exact same location, the end result that we hear is a new tone having the pitch of the lowest harmonic and a new and different tonality.
Harmonics are individual sine wave frequencies and each is an integral multiple of the basic, or fundamental frequency of the tone. Since all harmonics in a musical tone are locked together and all originate from the same source, we do not hear them as individual tones. Instead we hear a composite tone color or sound which we recognize as a particular voice, musical instrument, whistle, horn, etc. The reason why your voice sounds different from a clarinet is principally related to the harmonic content and structure of each. True, there are other factors which help to create the differences among various musical sounds, but the harmonic content is the most important one.
Figure 10. Two harmonically related sine wave pitches are superimposed or mixed. One has half the amplitude of the first and exactly twice the frequency.
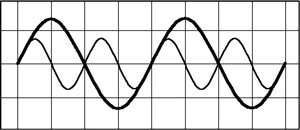
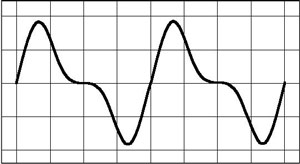
Figure 11. The actual result of mixing the two sine-waves together results in a new soundwave having a different shape as you see in this picture. The frequency or pitch is the same as that of the single sinewave in figure ten, but the shape is different, and as such it will sound different to us. This is how the Hammond organ produces multiple tone colors. It allows the musican to select individual harmonics and control their amplitudes.
The first harmonic is the basic frequency of the tone itself. The second harmonic has exactly twice the frequency of the first. The third harmonic has three times the frequency, and so on. If we produce a tone of A at 440 Hz, which is the pitch standard for all Western musical instruments, then the second harmonic is a frequency of 880 Hz, the third is 1320 Hz, the fourth 1760 Hz. A theoretically infinite number of harmonics is possible. In practice most tones with a lot of harmonic content, such as the sound from a loudly played trumpet or a truck horn rarely have more than 50 detectable harmonics.
At first it may seem hard to believe that when you hear a single trumpet note, for example, that you are actually hearing perhaps thirty or forty different yet related frequencies. But, it is the combination of these many harmonics which make the trumpet sound as it does and why it sounds completely different from the same note or pitch on a violin. Tones having very few harmonics sound “dull,” whereas tones having many harmonics sound “bright.”
The Hammond system allows the musician to control the actual individual harmonics or sine wave frequencies for a particular note on the keyboard so that he can (within the definite limits of the instrument) make multitudes of different final sounds. The process is called additive harmonic synthesis, where you combine simple sine wave frequencies in different proportions to mimic actual sounds which contain various combinations of harmonics.
Previous page Page 5. Next page