The HAMMOND ORGAN
North Suburban HAMMOND ORGAN Service
Producing an accurate series of fifty harmonics for all of the notes on two 61 note keyboards and either a 25– or 32 note set of bass pedals would make a tone wheel instrument enormously complex, prohibitively cumbersome and heavy, and extremely expensive. Therefore, Hammond and his people had to resort to many, many compromises. As it is, the average Hammond contains thousands of individual parts, so it is still a very complicated machine.
Laurens Hammond and his engineers studied real pipe organs and other instruments until they finally determined that having control over the first eight harmonics would give the Hammond sufficient tonal resources to develop suggestive imitative accuracy and versatility for general musical usage. Hammond also realized that since most of the lower harmonics either are exactly the same, or very close† in frequency to pitches of the normal equally tempered musical scale, he could use the same frequencies both as fundamentals for some notes and as harmonics of others, thus eliminating the need for a huge number of separate tone wheels and their associated parts.
Hammond also left out the seventh harmonic†, however he provided two “sub harmonics” related to a tone one octave lower than the fundamental for extra versatility for the musician. Therefore, each key of a Hammond is capable of sounding nine harmonically related sine wave frequencies. Furthermore, Hammond provided an ingenious system whereby the musician can regulate the relative volume of each harmonic from zero to full strength with eight degrees of loudness for each. Now let’s calculate what this means. If there are nine harmonically related frequencies available on each key, and each can be either fully off or at any one of eight different volume levels, then this becomes 9 to the ninth power or the amazing total of 387,420,489 possible different tonal combinations available on each playing key. Now that’s tonal versatility! However, many of the available tonal combinations sound very much like each other, and many others are octave duplications of the same thing. Some are also musically useless. In actuality, there are perhaps 500 truly distinct usable tonalities. Each of these, however, is capable of hundreds of subtle minor adjustments.
To make all of this possible, each playing key on the instrument operates a set of nine switching contacts under the key. Each contact carries one particular pitch or frequency. In schematic form, it looks like figure thirteen.
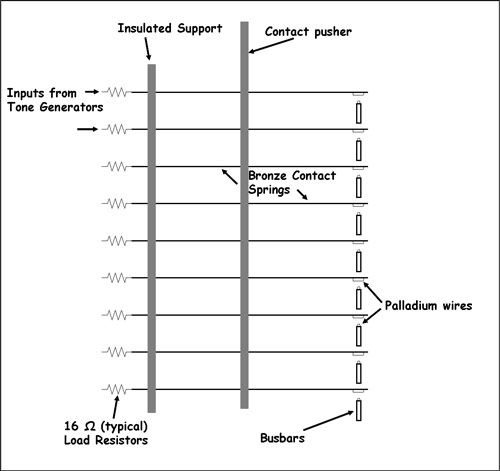
Figure 12. This partially diagrammatic drawing shows the arrangement under a typical key on a tonewheel Hammond. When you push down on a key, it moves the bakelite contact actuator down slightly which pushes the nine bronze contact springs down so that they contact the nine corresponding busbars which run lengthwise through the keyboards. Notice that each contact spring as well as the top of each busbar has a palladium wire attached which insures a good electrical contact.
The correct nine frequencies from the tone generator for each playing key are fed through isolation resistors to the nine key contacts. When you push a key, a bakelite actuator pushes the nine contacts down and they contact the horizontal busbars that run the entire length of the keyboard.
The busbars convey the signals to the harmonic drawbars, a series of sliding controls that can connect each busbar selectively to either ground or to one of eight taps on the primary of the matching transformer.
The secondary of the matching transformer conveys the resulting signal to the input stage of a preamplifier for amplification and further processing. Let’s return for a moment to the key contacts. A typical Hammond keyboard is a standard, 61 note organ keyboard. Each key has nine contacts. Therefore, the entire keyboard has 61 × 9 contacts or 549 contacts in all, each carrying one frequency.
Because there are only 91 available frequencies from the tone generator, it is evident that the same frequencies must appear on a number of different key contacts, which is indeed the case. (Remember the compromises Laurens Hammond needed to make his invention commercially practical?) Since the same frequencies appear on a number of contacts, and since several of these may be closed at one time (depending on the musician’s settings and playing requirements at any moment) and also because the tapped primary winding of the transformer mentioned above has extremely low impedance, it is necessary to put a small isolation resistor in series with each contact.
In the Hammond, these resistors are actually lengths of resistance wire which are connected between the tone generator input terminals of a keyboard and the appropriate key contacts. Without the resistors, if any keyboard busbar’s signal selector (drawbar) was “off” or grounded, the entire output of one or more tone wheels could be shorted to ground and would not be available on any of the other contacts where it might be simultaneously needed. Thus Laurens Hammond found right from the start that resistors were absolutely necessary in his key contact assemblies.
† With the exception of octave-related harmonics such as 1, 2, 4, 8, etc. all of the other harmonics (such as 3,5,6,7, etc.) do not correspond exactly to the notes of the scale. The 3rd, 6th, and 9th harmonics are very close, however, and tempered scale pitches can be used with essentially no noticeable discrepancy. In the case of the 5th harmonic, the closest tone available on the tempered scale is 14% sharper in pitch than the true fifth harmonic for any particular tone, however, in an instrument like the Hammond, it is close enough to be acceptable. When we look at the seventh harmonic, however, we find that the true seventh harmonic is just about 30% flatter than the closest equivalent pitch from the tempered scale. Laurens Hammond felt that this was too much of an error, which is why he left the seventh harmonic out entirely. Some models of the Hammond, such as the H series and the X66 included a seventh harmonic, the feeling being that, because these instruments would probably be used with the vibrato ON most of the time, it would work. In my personal opinion, the seventh harmonic when derived from the tempered scale, in spite of its nearly 30% error, does indeed work and adds much to some of the effects which are available on these newer Hammond models.
Previous page Page 6. Next page